순열과 조합은 코딩 테스트에서 자주 등장하는 개념으로, 데이터를 나열하거나 선택하는 문제를 해결하는 데 필수적이다. 이러한 개념을 이해하고 활용하면 효율적인 알고리즘 설계와 문제 해결에 큰 도움이 된다. 오늘은 순열과 조합에 대해 개념과 코드에 대해 알아보도록 하겠다.
순열(permutation)

순열(permutation): 여러 개의 요소를 특정 순서에 따라 배열하는 경우의 수

예를 들어, 3개의 숫자 1, 2, 3을 모두 사용해 순열을 구하는 경우 P(3, 3) = 3! = 6이 되어 6가지 경우의 수가 나온다.
- (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)
시간 복잡도는 얼마일까?
O(n!)이다. n개의 요소가 있다면 첫 번째 자리를 선택하는 경우의 수는 n가지이다. 그 후로 n - 1, n - 2, ... 이렇게 마지막 요소까지 이어진다. 따라서 n x (n - 1) x (n - 2) x ... x 1 = n!이 된다.
이제 순열을 코드로 구현하는 방법을 살펴보자.
순열 구현: 재귀
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void permutation(vector<int>& arr, int depth) {
if (depth == arr.size() - 1) {
for (auto i : arr)
cout << i << ' ';
cout << '\n';
return;
}
for (int i = depth; i < arr.size(); i++) {
swap(arr[depth], arr[i]);
permutation(arr, depth + 1);
swap(arr[depth], arr[i]);
}
}
int main() {
vector<int> arr = vector<int>({1, 2, 3});
permutation(arr, 0);
return 0;
}
코드 실행 결과

재귀 함수 분석
- 기저 사례: depth가 arr.size() - 1에 도달하면 하나의 경우를 의미하므로 해당 경우를 출력한다. arr.size()에서 1을 빼는 이유는 마지막 요소에 대해선 처리할 필요가 없기 때문이다.
- 재귀 사례: arr의 요소를 depth에 따라 swap 처리한다. 이때 다시 swap을 수행하여 복원하는 과정이 필요하다.
재귀 함수를 이해하기 힘들다면 직접 노트에 그래프를 순회하는 과정을 그려서 확인해보면 좋다.
혹은 next_permutation 함수를 사용하여 구현할 수 있으니 참고하도록 하자.
순열 구현: next_permutation
#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
using namespace std;
int main() {
vector<int> vec = vector<int>({1, 3, 2});
set<vector<int>> unique_permutations;
// 정렬 필수!
sort(vec.begin(), vec.end());
do
{
vector<int> subset(vec.begin(), vec.end());
unique_permutations.insert(subset);
} while(next_permutation(vec.begin(), vec.end()));
for (auto subset : unique_permutations) {
for (auto ele : subset)
cout << ele << ' ';
cout << '\n';
}
return 0;
}
코드 실행 결과

#include <algorithm> 을 추가하면 next_permutation 함수를 사용할 수 있다.
이 함수를 통해 컨테이너의 요소를 swap하며 순열을 구현할 수 있다.
단, 컨테이너는 반드시 정렬된 상태여야 한다.
또한, set 컨테이너를 활용하여 중복되는 값을 방지할 수 있다.
조합(combination)

조합(combination):여러 개의 요소를 순서에 상관 없이 배열하는 경우의 수

예를 들어, 3개의 숫자 1, 2, 3 중에서 2개를 선택하여 조합을 구하는 경우 C(3, 2) = 3! / (2! x 1!) = 3이 되어 3가지 경우의 수가 이 나온다.
- (1 - 2), (1 - 3), (2 - 3)
시간 복잡도는 얼마일까?
O(2^n)이다. 조합을 구하는 과정에서는 각 요소에 대해 "선택"하거나 "선택하지 않기"의 두 가지 경우가 존재하기 때문이다.
이제 조합을 코드로 구현하는 방법을 살펴보자.
조합 구현: 재귀
#include <iostream>
using namespace std;
int arr[5] = { 1, 2, 3, 4, 5 };
bool isVisited[5] = { false };
void combination(int n, int r, int cur, int depth) {
if (depth == r) {
for (int i = 0; i < n; i++)
if (isVisited[i])
cout << arr[i] << ' ';
cout << '\n';
}
for (int i = cur; i < n; i++) {
if (isVisited[i]) continue;
isVisited[i] = true;
combination(n, r, i, depth + 1);
isVisited[i] = false;
}
}
int main() {
combination(5, 3, 0, 0);
return 0;
}
코드 실행 결과
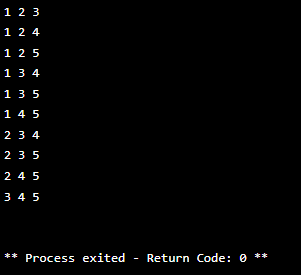
재귀 함수 분석
- 기저 사례: depth가 r에 도달하면 하나의 경우를 의미하므로 해당 경우를 출력한다. 이때, isVisited 된 부분만 출력하여 경우를 표현한다.
- 재귀 사례: 모든 번호에 대해 특정 번호를 방문할 수 있다면 isVisited를 마킹하고 재귀로 들어간다. 재귀가 끝다면 isVisited를 복원시킨다. 이때, 반복문의 시작은 최근 마킹한 번호로 지정한다.
혹은 중복 for문을 사용하여 구현할 수 있으니 참고하도록 하자.
순열 구현: 중복 for문
#include <iostream>
using namespace std;
int main()
{
int n = 5;
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
for (int k = j + 1; k <= n; k++)
cout << i << ' ' << j << ' ' << k << '\n';
}
코드 실행 결과
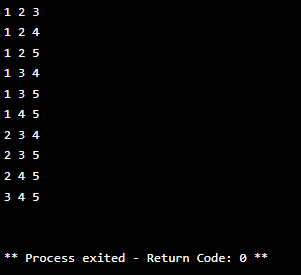
반복 for문은 뽑는 개수가 늘어날수록 반복문이 늘어나기 때문에 좋은 방법은 아니다.
그 외에도 비트마스크를 사용하여 구현할 수도 있지만, 이 개념은 추후에 따로 다루도록 하겠다.
정리
오늘은 탐색에서 가장 기본이 되는 순열과 조합에 대해 알아보았다. 코딩 테스트 혹은 알고리즘에서 탐색은 매우 중요하기 때문에 개념과 시간 복잡도, 코드를 잘 기억하면 좋다.
'IT > 알고리즘' 카테고리의 다른 글
| [이론] 그래프 (Graph) (1) | 2024.11.08 |
|---|---|
| [이론] 완전 탐색과 백트래킹 (0) | 2024.11.07 |
| 코딩 테스트에서 C++이 유리한 이유와 장점 (3) | 2024.11.04 |
| [C++] 최소 신장 트리(MST) (0) | 2023.11.16 |
| [C++] 플로이드-워셜(Floyd-warshall) (0) | 2023.11.16 |